mekanika teknik

CONTOH HITUNGAN MEKANIKA TEKNIK

Dibawah ini saya sajikan contoh perhitungan suatu konstruksi dengan beban merata berbentuk segitiga dan beban terpusat dari berbagai arah:
Diketahui suatu gambar struktur denagan tumpuan sendi dan rol sebagai berikut:

MENGHITUNG REAKSI TUMPUAN

ΣMB = 0
-( ½ x 2 x 2 ) x 6.6667 + RAv x 6 – ( 1×6) x 3 + (4×2) – ( 4×1)          =0
-13.3334 + 6 RAV – 18 + 8 – 4                                                           =0
6 RAv  - 27.3334                                                                     =0
RAv = 27.3334 / 6

Kontrol ΣV = 0RAv + RBv = 1/2×2×2 + 1×6 +4 4.5556 + 7.4444 =     12 ton ( O.K )

= 4.5556 ton
ΣMA = 0
-4 x 1 + (4×8) – RBv x 6 + (1×6)x3 +  4×2 – (4 x1)                =0
-4 + 32 – 6RBv – 18 – 1.3334                                                 =0
- 6 RBv + 44.6666                                                                   =0
RBv = -44.6666 / -6
= 7.4444 ton

MENGHITUNG BIDANG M ( MOMEN )

M 2m   = – ( 1/2 x 2 x 2 ) x 0.6667
= – 1.3334 ton
M 5m   = – ( 1/2 x 2 x 2 ) x 3.6667 + RAv x 3 – ( 1 x 6 )  x 1.5
= -7.3334 + 13.6668 – 9
= -2.6666 ton
M 8m   = – ( 1/2 x 2 x 2 ) x 6.6667 + RAv x 6 – ( 1 x 6 )  x 3
= -13.3334 + 27.3336 – 18
= -3.9998 ton
M 10m = – ( 1/2 x 2 x 2 ) x 8.6667 + RAv x 8 – ( 1 x 6 )  x 5 + 4
= -17.3334 + 36.4448 – 30 + 14.8888 + 4
= 0 ton

MENGHITUNG BIDANG Q ( GAYA LINTANG )

Q 2m   = -( 1/2 x 2 x 2 ) +RAv
= – 2 + 4.5556
= 2.5556 ton
Q 8m   = -( 1/2 x 2 x 2 ) +RAv – (1 x 6)
= – 2 + 4.5556 – 6
= -3.4444 ton
Q 10m = -( 1/2 x 2 x 2 ) +RAv – (1 x 6) + RBv – 4
= – 2 + 4.5556 – 6 + 7.4444 – 4
=  0 ton

MENGHITUNG BIDANG N ( GAYA NORMAL )

RBh – ( 4 x 1 )             = 0
RBh                 = 4 ton
tolong di koreksi kalu ada yang salah bisa masukin dibawah

Mekanika teknik pada konstruksi gerber

Dalam perhitungan mekanika teknik konstruksi gerber, sebelumnya struktur kita pecah dahulu menjadi bagian yang kecil – kecil sehingga dapat di hitung momen yang bekerja di dalamnya.
Contohnya seperti sebuah gambar struktur sebagai berikut:

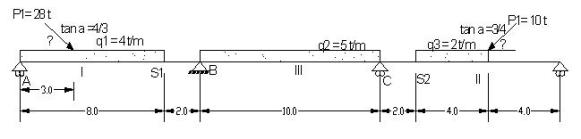
MENGHITUNG REAKSI TUMPUAN

kontruksi A – S1 KiriΣMS1 = 0 -RAvx8 – 22.4×5 – (4×8)x4     = 0 -8 Rav -112 – 128                    = 0 Rav = 240 / 80 = 30 ton

ΣMA = 0S1×8 + (4×8)x4 + 22.4X3        = 0 8S1 -128 – 67.2                       = 0 RS1v = -192 / -8 = 24.4 ton

Kontrol ΣV = 0
22.4 + ( 4 x 8 ) = 30 + 24.4
54.4 ton        =  54.4 ton       ( O.K )

Konstruksi S2 kanan – DΣMD = 0 -S2×8 – (2 x4)x6  – 6×4         = 0 -8 S2 -48 – 24                         = 0 RS2v = 72 / 8 = 9 ton

ΣMS2 = 0-RDvx8 + 6×4 + (2×4)x2          = 0 -8RDv +24 + 16                       = 0 RDv = -40 / -8 = 5 ton

Kontrol ΣV = 0
( 2 x 4 ) + 6  = 9 + 5
14 ton        =  14 ton       ( O.K )

Konstruksi S1 kanan – S2 kiriΣMC = 0 -S1×12+RBvx12–(5×10)x5+S2×2 = 0 -24.4×12+10RBv-250+ 9×2          = 0 RBv = 524.8 / 10 = 52.48 ton

ΣMB = 0S2X12-RCvx10-(5×10)x5-S1×2 = 0 9×12-10RCv+250-24.4×2                      = 0 RCv = -309.2 / -10 = 30.92 ton

Kontrol ΣV = 0
24.4 + 50 + 9  = 52.48 + 30.92
83.4 ton        =  83.4 ton       ( O.K )

MENGHITUNG BIDANG M ( MOMEN )

momen titik sehauh 3 m dari titik AM 3m   = RAv x 3 –( 4×3) x 1.5 = 30×3-12×1.5 = 42 t.m Momen sejauh 8 m dari titik A M 8m   = RAv x 8 –( 4×8) x 4-22.4×5 = 30×8-128-112 = 0 t.m Momen sejauh 10 m dari titik A .M 10m             = – S1 x 2 = -24.4 x 2 = – 48.8 t.m Momen sejauh 15 m dari titik A M 15m             = – S1 x7+ RBvx5 – ( 5×5 ) x2.5 = 24.4 x 7 + 52.48 x 5 – 25 x 2.5 = 29.1 t.m

Momen sejauh 20 m dari titik AM 20m             = – S1 x 12 +RBv x 10 –( 5×10) x 5 = -24.4 x12+52.48 x 10 – 50×5 = -18 t.m Momen sejauh 22 m dari titik A M 22m             = – S1 x 14 +RBv x12 –(5×10)x7 + RCv x 2 = -24.4×14 + 52.48 x12-50×7 + 30.92×2 = 0 t.m Momen sejauh 26 m dari titik A M 26m             = – S2 x 4 – (2×4) x 2 = 9 x 4 – 8 x 2 = 20 t.m Momen sejauh 30 m dari titik A M 30m             = – S2 x8 – ( 2×4 ) x6 – 6×4 = 9 x 8 + 8 x 6 – 6 x 4 = 0 t.m

MENGHITUNG BIDANG Q ( GAYA LINTANG )

gaya lintang ditik AQ 0m   = RAv = 30 ton Gaya lintang sejauh 3 m dari titik A Q 3m   = RAv – ( 4×8 ) – 22.4 = 30-32-22.4 = -4.4 ton Gaya lintang sejauh 8 m dari titik A Q 8m   = RAv – ( 4×8 ) – 22.4 + S1 = 30-32-22.4+24.4 = 0 ton Gaya lintang sejauh 10 m dari titik A Q 10m             = – S1 + RBv = -24.4+52.48 = 28.08 ton Gaya lintang sejauh 15 m dari titik A Q 15m             = – S1+ RBv – ( 5×5 ) = -24.4 + 52.48 – 25 =  3.08 ton

Gaya lintang sejauh 20 m dari titik AQ 20m             = – S1+ RBv – ( 5×10 ) + RCv = -24.4+52.48-50+30.92 =  9 ton Gaya lintang sejauh 22 m dari titik A Q 22m             = – S1+ RBv – ( 5×10 ) + RCv – S2 = -24.4+52.48-50+30.92 – 9 =  0 ton Gaya lintang sejauh 26 m dari titik A Q 26m             = S2 – (2×4) -6 = 9 – 8 – 6 = -5 ton Gaya lintang sejauh 30 m dari titik A Q 30m             = S2 – (2×4) -6 + RDv = 9 – 8 – 6 + 5 = 0 ton

MENGHITUNG BIDANG N ( GAYA NORMAL )

Gaya normal ditik B
RBH + 16.8 – 8             = 0
RBH +8.8 ton              = 0
RBH    = – 8.8 ton

Perhitungan Mekanika Teknik Antara Program Struktur SAP 2000 Dengan Perhitungan Manual

Sudah lama saya menggunakan program analisis struktur SAP 2000 tetapi masih tetap menjadi penasaran bagi saya. Mengapa? Karena yang namanya program komputer merupakan program terapan atau terpakai. Jadi kita tinggal memakainya saja tanpa pusing-pusing lagi melewati proses perhitungan yang membutuhkan waktu lama. Penasarannya apakah hasilnya itu juga sesuai dengan hasil jika proses dihitung secara manual? Nah ini mungkin bisa menjadi jawabannya... Misalnya.....

Diketahui: Suatu konstruksi seperti tergambar di atas.

Ditanya: Gambarkan SFD dan BMD.

Penyelesaian:

EMA = 0

-10 . RBV + 5 . 5 + 1 . 10 . 5 = 0

10 RBV = 75

RBV = 7,5 t

EMB = 0

10 . RAV – 5 . 5 – 1 . 10 . 5 = 0

10 RAV = 75

RAV = 7,5 t

Cheking :

EV = 0

RAV + RBV – 5 – 1 . 10 = 0

7,5 + 7,5 – 15 = 0 (OK)

Momen :

MI = RAV . 5 – 1 . 5 . 1/2 . 5

= 7,5 . 5 – 1/2 . 1 . 25 = 37,5 – 12,5 = 25 tm

Penggambaran SFD dan BMD 

Kemudian dianalisis dengan Program SAP200, hasilnya sebagai berikut:

Penggambaran situasi beban-beban yang ada 

Penggambaran hasil SFD dan BMD

SFD

BMD

Nah...ternyata perhitungan manual dengan analisis struktur dengan program SAP2000 hasilnya sama.

Perlu diingat bahwa beban mati yang ada pada material dianggap tidak ada atau dikalikan dengan 0, seperti kolom isian yang ada di bawah ini:

Jadi nggak usah ragu lagi menggunakan program SAP2000 memang OK!